Bronsted-Lowry Acid-Base Equilibrium
In this lesson, I want to talk about the fundamentals of the acid-base equilibrium and how we use it within the scope of organic chemistry. But before we go into the details of the acid-base equilibrium itself, let’s review what a base and what an acid is according to different definitions. There are three most common definitions of acids and bases and the simplest one, perhaps, is the Arrhenius definition.
Arrhenius Acids and Bases
According to the Arrhenius definition, proposed by the Swedish physical chemist Svante Arrhenius, an acid is a donor of a proton (H+) while the base is a donor of the hydroxyl ion (OH–). A typical example of an Arrhenius acid is something like hydrochloric acid (HCl). While a typical example of an Arrhenius base is something like sodium hydroxide (NaOH). Once those species dissociate, HCl gives H+ into the solution, while NaOH gives off the OH– ion.
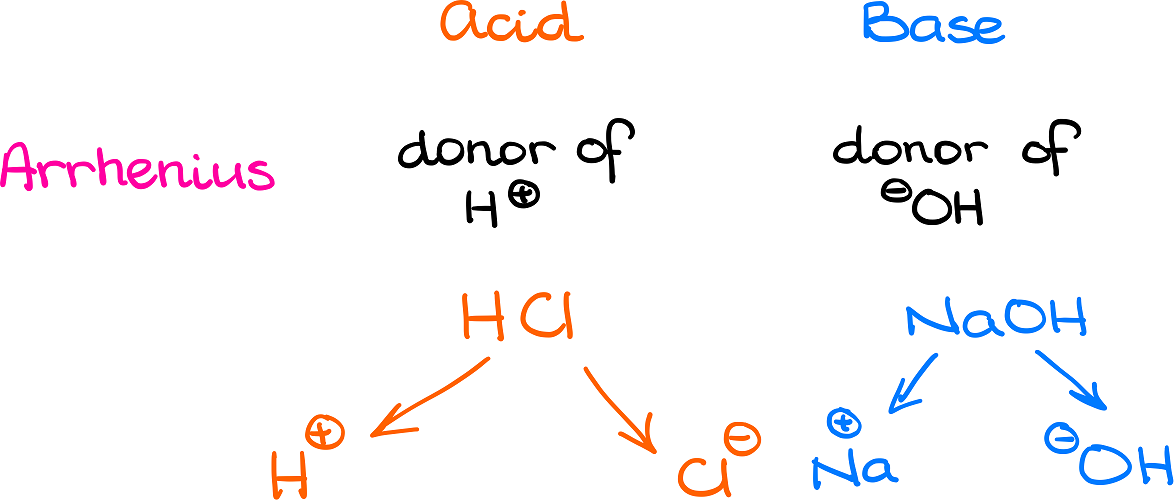
The problem with this definition is that it is extremely limited in its scope and is only applicable towards aqueous solutions. In organic chemistry, however, we rarely deal with aqueous solutions. Thus, this definition doesn’t work for our purposes.
Brønsted-Lowry Acids and Bases
Danish physical chemist Johannes Brønsted and English physical chemist Thomas Lowry proposed a more general acid base definition. According to the Brønsted-Lowry theory, an acid is a donor of H+, while a base is an acceptor of H+. This way, the theory can be expanded onto acids and bases in any media and is not limited to just aqueous solutions.
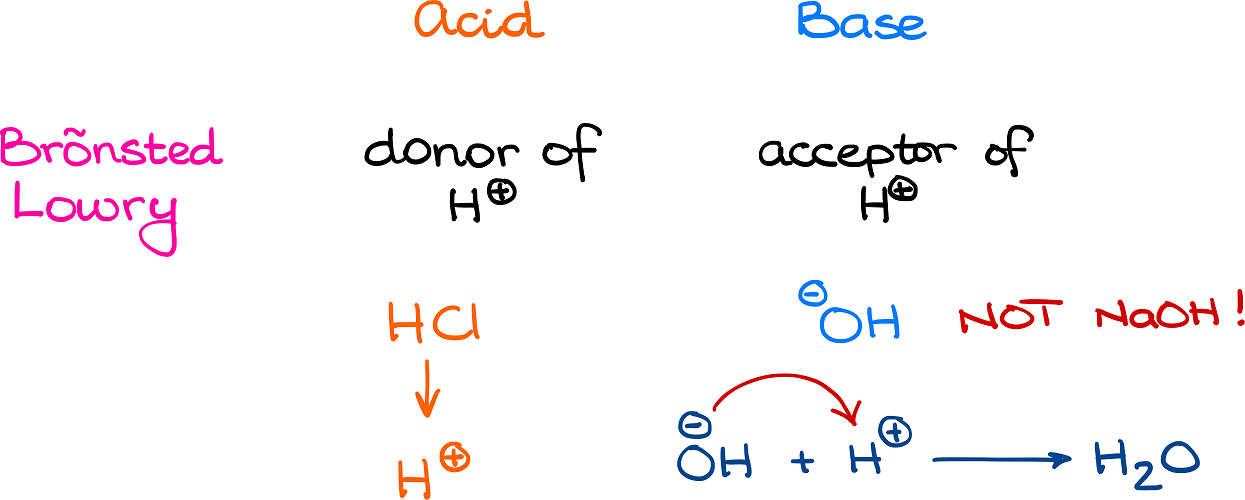
Thus, a Brønsted acid is the same species as the Arrhenius acid. However, when it comes to a base, only the species that accepts the proton is the base. So, in sodium hydroxide (NaOH) only OH– is the base and not the entire molecule. This is a very common mistake, so you can expect some trickery around this definition in the exam.
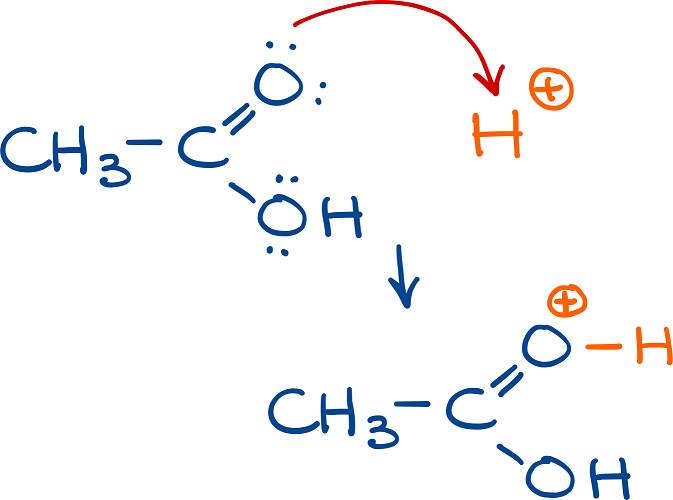
Also remember, that if a species accepted a proton, it’s a base, regardless of how we are used to think about it. For instance, if we take an acetic acid and protonate it (add a proton to it), then the acetic acid acts as a base in such a reaction.
Conjugate Acids and Bases
The Brønsted-Lowry theory also describes the relationship between the reagents in an acid base reaction and the products. The products in an acid base reaction are called the conjugates. Let’s take for example a reaction between methyl acetate (an ester) and sulfuric acid. In this reaction the ester acts as a base by accepting a proton and sulfuric acid acts as Brønsted acid by providing said proton. Once our ester (which is a base on the reagent side) accepts the proton, it becomes a conjugate acid. Likewise, once sulfuric acid loses the proton, it becomes a conjugate base.
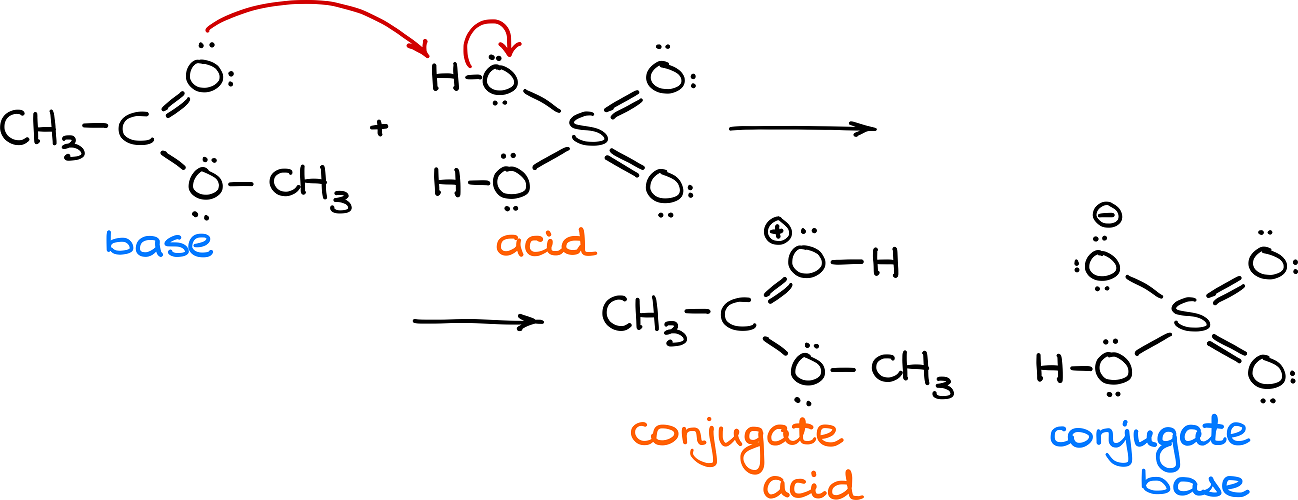
Thus, once an acid loses the proton, it becomes a conjugate base. And once a base accepts a proton, it becomes a conjugate acid. Remember, that when we are talking about the conjugates we are always talking about the products of a specific acid-base reaction. The conjugate base that we made in the reaction above (HSO4–) can dissociate further and be an acid in a different reaction. But in this particular case, the HSO4– ion is a conjugate base.
Lewis Acids and Bases
There’s one last even more general acid base theory proposed by the American physical chemist Gilbert Lewis. His acid-base theory is sometimes called the electronic theory of acids and bases. According to the Lewis theory, an acid is an electron pair acceptor, while a base is an electron pair donor.
For the purposes of this lesson, I am not going to go any further into the details of the Lewis theory and leave it for another lesson. For the rest of this discussion though, I’ll be focusing solely on the Brønsted-Lowry theory of acids and bases.
Strong Acids vs Weak Acids
Now, when we know what the acids and bases are, let’s talk a little bit about the qualitative difference between those. Namely, I want to look at the difference between strong acids and weak acids.
When we say that the acid is strong, we mean that said acid dissociates completely in a solution. Likewise, if the acid is weak, it will only dissociate partially.

Well, what exactly does it mean? Let’s look at these two examples:
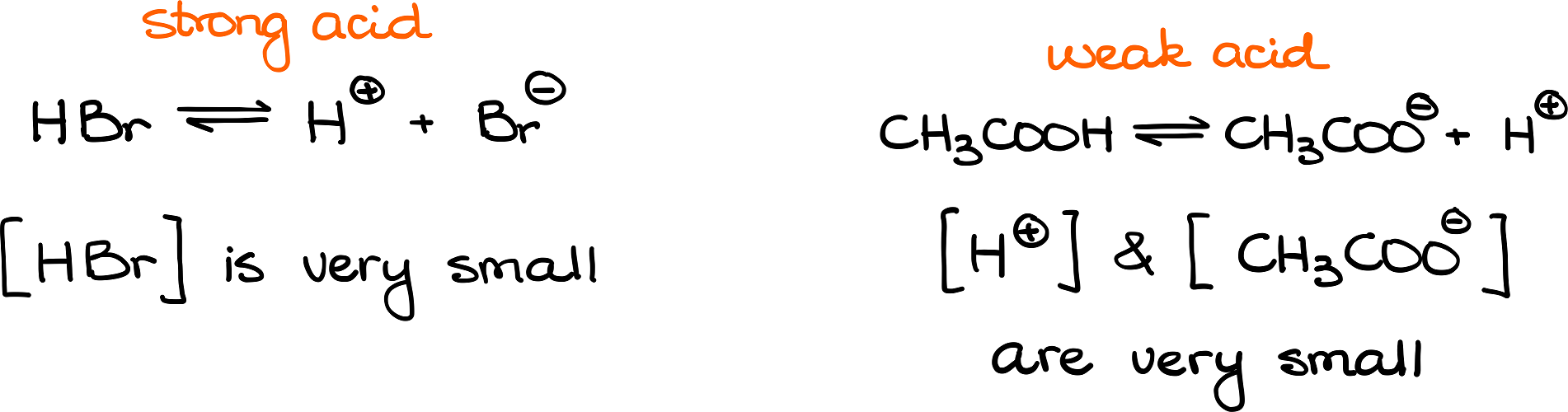
On the left side I have hydrobromic acid (HBr), which is a very strong acid. While on the right side—acetic acid (CH3COOH) a typical weak acid. When a strong acid dissociates completely, it means that we will have virtually no HBr left in the solution. While, on contrary, when acetic acid dissociates, it won’t give us much of the dissociation products and will predominantly stay as is.
How Do We Quantify Acid Strength?
Saying that one acid is strong while the other one is weak is a little bit of handwaving. So, is there a way how we can quantify the “strong” and the “weak” using some sort of numeric value?
We use the acid dissociation constants (Ka values) for this purpose. By the definition, the dissociation constant for an acid equals to the ratio of the product concentrations over the concentration of reagents.
Let’s look at it on the example of dissociation of HCN:
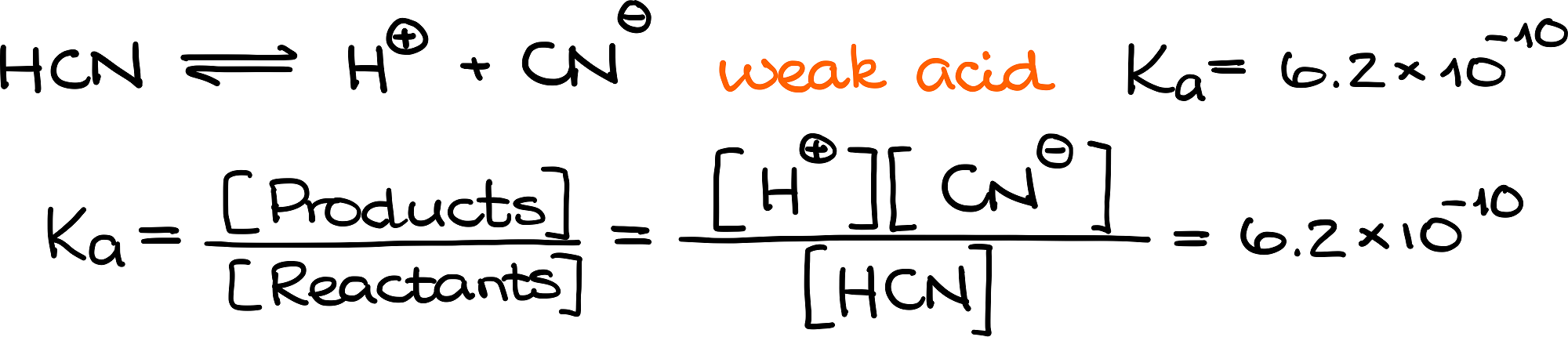
Hydrogen cyanide is a weak acid and only dissociates partially. The reagent in this case is the acid itself (HCN). While the products are the proton (H+) and the cyanide anion (CN–). We now can get the expression of the dissociation constant by putting the concentrations of these species into the equation for Ka. And since the hydrogen cyanide is a weak acid, we’ll have only a very small quantity of our products. This results in a very small Ka value.
How to Read the Ka Values?
Since the Ka is a mathematical expression for the state of equilibrium, it is quite easy to interpret. If the Ka value is small, we don’t have much of our products. No products means no dissociation. No dissociation means weak acid. Likewise, a large Ka value means tons of products. Tons of products means complete dissociation. Complete dissociation means strong acid. Quite straightforward.
The issue with the Ka values is that those are generally very ugly numbers that are difficult to work with, yet alone—remember. So, typically, we are going to be using the pKa values instead. By definition, the pKa value is a negative logarithm of the Ka value. It doesn’t have any physical meaning outside of the convenience.
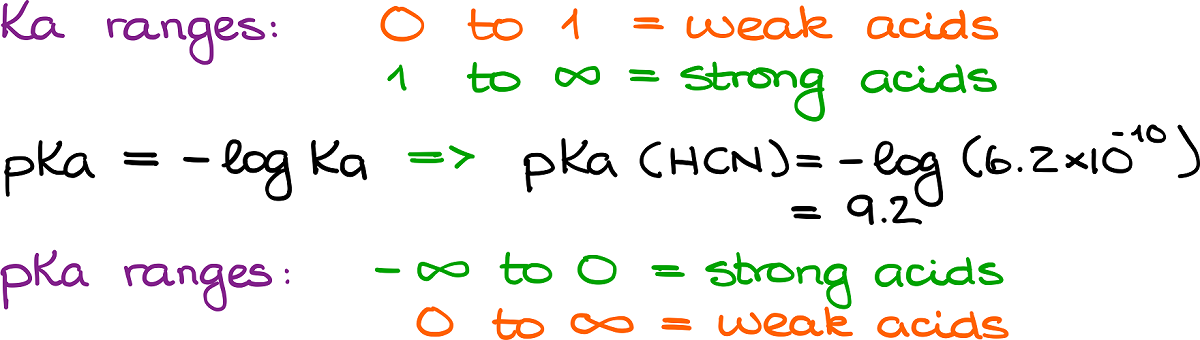
The important feature of the pKa scale is that it is inverted compared to the Ka scale. Thus, strong acids will have a negative pKa values, while weak acids will have positive pKa values.

Examples of the pKa Values and How We Can Use Them
Let’s look at a few species so we can see how the Ka and the pKa values compare to each other.
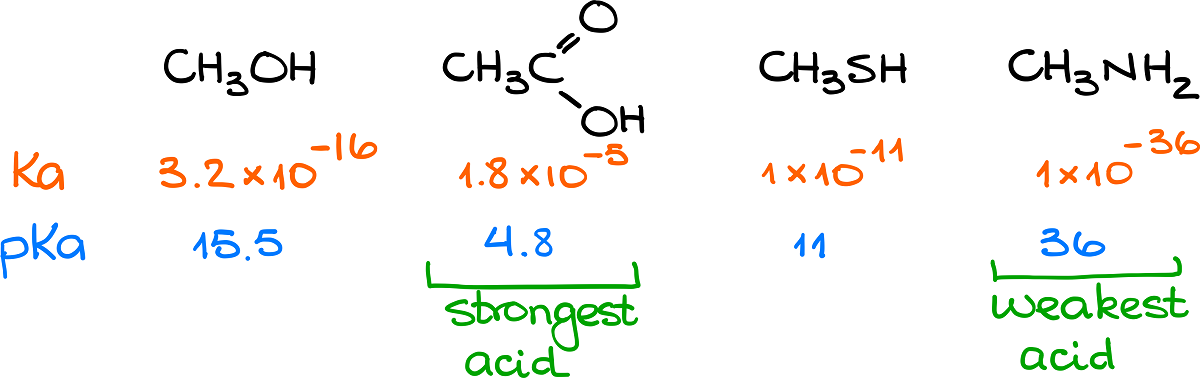
On this picture we have methanol, acetic acid, methanethiol, and methylamine. Next to each of these species we have their corresponding Ka and pKa values. By doing a quick comparison of those numbers, we can see that the acetic acid the strongest acid among these molecules. Meanwhile, the amine species at the very end is the weakest acid with the lowest Ka value and, correspondingly highest pKa value. Thus, if we wanted to, for instance, rank those molecules according to their acid strength from the weakest to the strongest, we’d get the following:
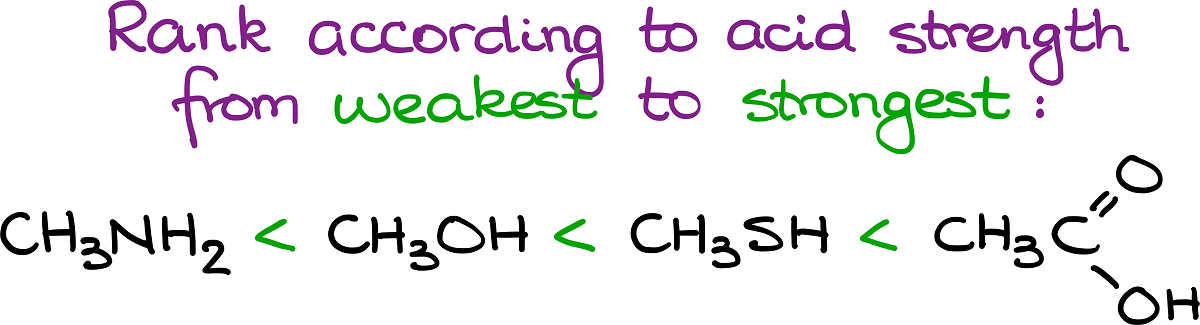
Questions like this one are fairly common on exams, so you may want to do some extra practice to be all prepared on the test.
Using pKa Values to Predict the State of Equilibrium
Now, we’ve used the Ka and pKa values to rank the acid strength. What else can we do with those?
Well, another typical question you’re going to see on the test is the “predict the state of equilibrium” type of a question. You’ll have a reaction of some sort and you’ll need to reason your way with the pKa values and figure out if your reaction favors products or reagents.
How would you approach a question like that? It’s actually a fairly simple problem.
- First, you’ll need to identify the acid and a conjugate acid in your reaction.
- Then, find the corresponding pKa values in your pKa table.
- And finally, compare those values. The equilibrium always favors the weaker acid!
Look at these two examples here:
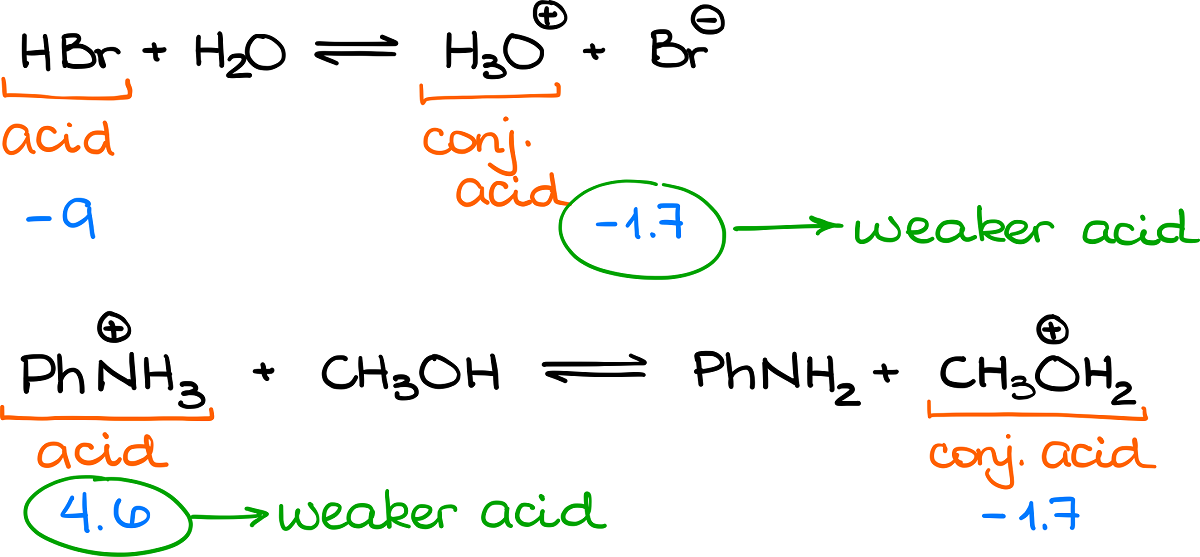
In the first case, the conjugate base has a lower pKa value, thus the equilibrium favors the products. In the second example, the reagent acid has a lower pKa value, making it a more favorable species, thus equilibrium favors the reagents.
Using The pKa Values to Estimate the Keq of the Reaction
Finally, we can use the pKa values to estimate the equilibrium constant for the reaction itself. It is, essentially, the same as telling which side of the reaction the equilibrium favors but in a quantitative (aka numeric) fashion.
For instance, let’s look at this reaction:

The first thing we would need to do is to find the acid and the conjugate acid. Then we’ll find the pKa values for those. We know that acid loses the proton in an acid-base reaction, so obviously the acetylene species on the left is our acid. And since the NH2– accepted that proton, NH3 is the conjugate acid.
Finding those in my pKa table gives me the following numbers:
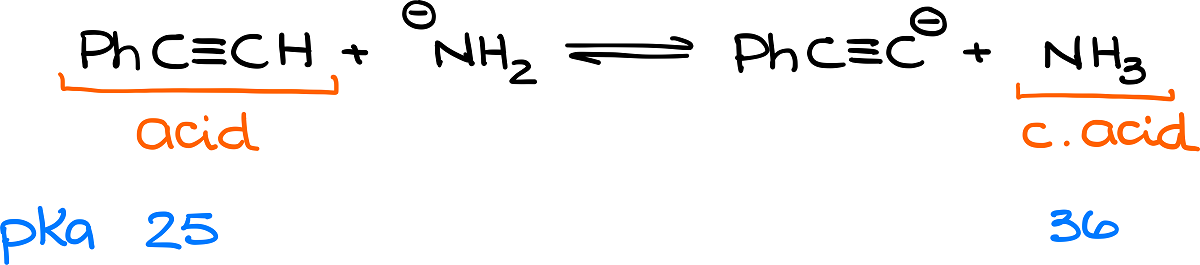
Based on our conversation from a few moments back, we already know that this equilibrium favors the products since the pKa value for my conjugate acid is 36 compared to 25 for the original acid. But how much is this equilibrium shifted, exactly?
Here’s a trick: we can easily estimate the equilibrium constant by taking 10 raised to the power of pKa for my conjugate acid minus the pKa for the original acid. I’m not going to bore you with the details of how this is obtained. I’ll show the exact detail in another post or you can see the derivation in my acid-base notes.
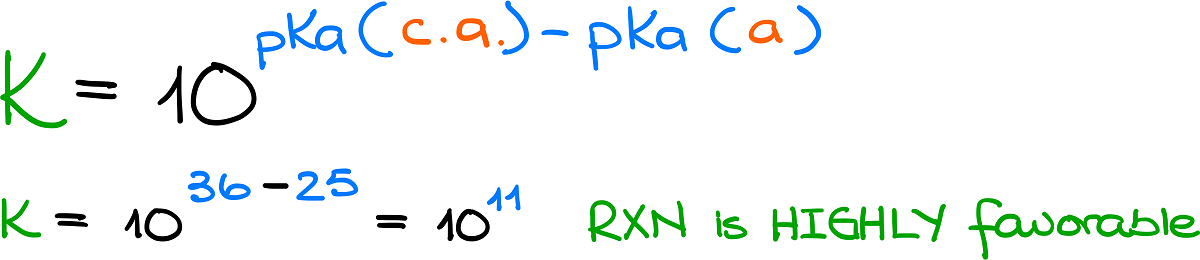
This calculation for this specific example yields 1011, which indicate a highly favorable reaction. Thus, if before we knew that the equilibrium favored the products, now we know the ratio between the products and reagents and it’s 1011!
Here’s another example:
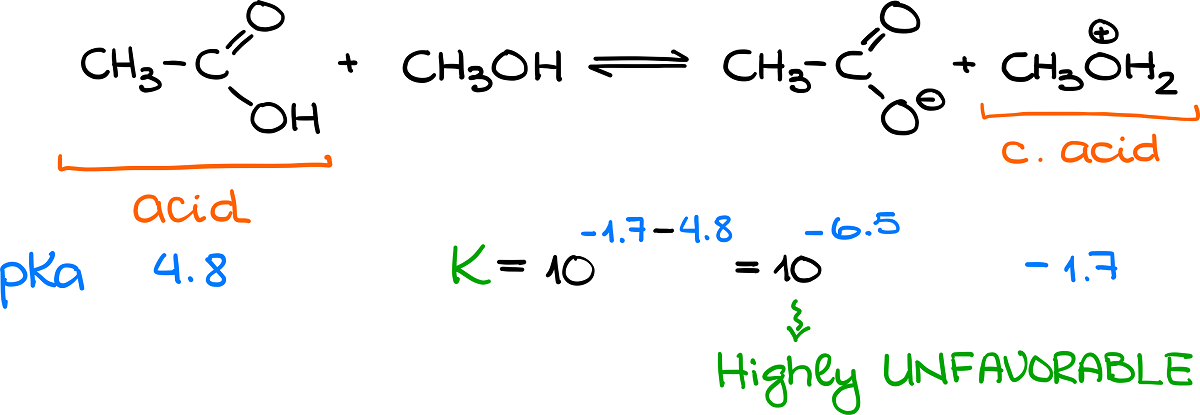
In this case, we have an original acid, which is much weaker than the conjugate acid. So, we know that the equilibrium will be shifted towards the reagents and the reaction is unfavorable. However, by plugging values into the formula I showed you a moment ago, we can see that the equilibrium constant here is 10-6.5. And we know that a small number for the equilibrium constant relates to an unfavorable reaction.
Become Familiar with Your pKa Table
We’ve been using the pKa values quite extensively in this lesson. So, I want to emphasize how important it is to become familiar with your pKa table. Most instructors will provide you with some sort of a pKa table on the exam. There are some, however, that will make you memorize the typical values and give you nothing. Make sure you know what to expect and find out ahead of time if you’ll have a pKa table on the test!
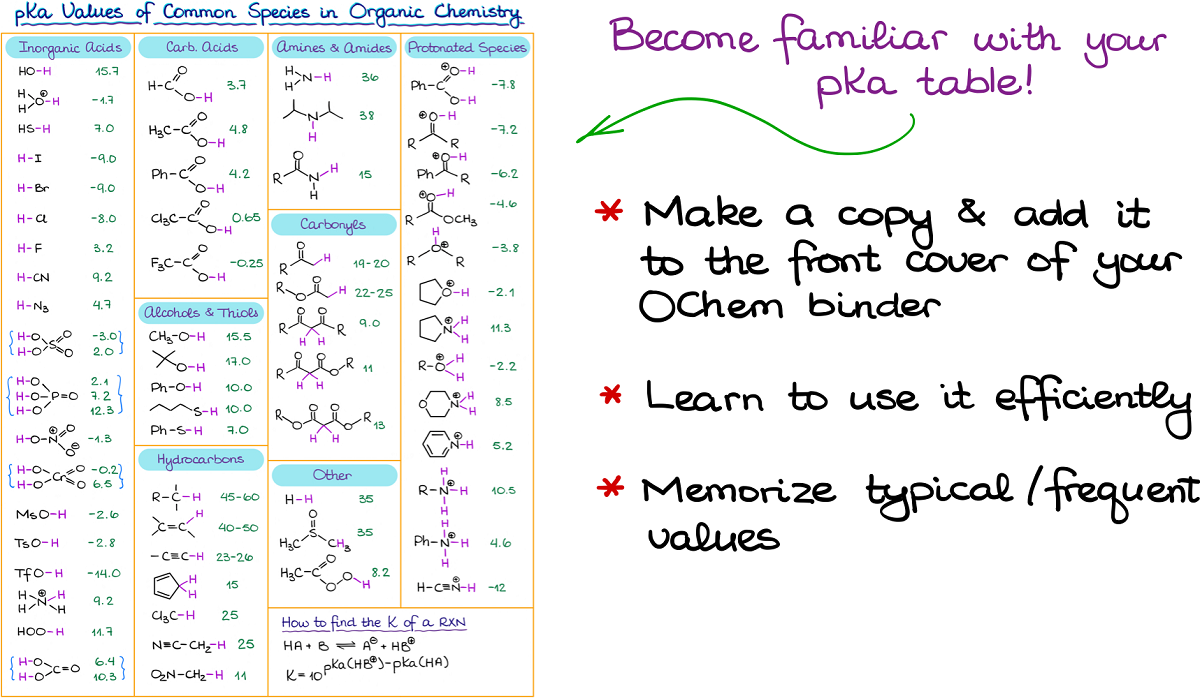
I suggest you make a copy of the table your instructor uses and put it under the front cover of your organic chemistry binder. This will save you a ton of time when you need to quickly look up the pKa values. And trust me, you’ll be looking up pKa values quite often in this course!
Next, make sure you know how to use your table. Some instructors like to use the pKa table with species arranged according to the pKa values. Personally, I hate those since they are really difficult to navigate. There is another type in which the table is arranged according to the functional groups. This, in my opinion, is the better version since you can easily navigate it knowing what compound and what functional groups you have in front of you.
Finally, I strongly encourage you to memorize the typical pKa values for the most common functional groups. While most instructors will tell you that there’s no need to memorize anything, this is not entirely true. Yes, you’re probably going to have a pKa table available to you on the test. But imagine if you had to reread your coffeemaker instructions every morning when you wanted to make a cup of delicious coffee. Wouldn’t it be a terrible waste of time and an inconvenience (especially if you’re as grumpy in the morning as I am before I’ve had my first cup). You definitely wouldn’t want that. Same deal with the pKa table. If you have to poke into the table every single time you want to double check a pKa value for something like a carboxylic acid or an alcohol, you’ll be wasting a lot of precious time on the test. And few moments here plus few moments there do add up.
Now, this was just the tip of the iceberg of what the acid-base equilibrium can look like. In the next lesson we’ll talk more about various typical exam questions and how to approach those.
