Examples of MO’s in Typical Conjugated Systems
The most common conjugated systems you’re going to see in your course are the allylic system, butadiene, pentadienyl ions, and hexatrienes. Let’s look at how the MO’s of those systems looks like. You’ll need to recreate and recognize these MO’s in your course, so make sure you practice drawing those.
Molecular Orbitals in Butadiene
The butadiene-type system consists of two conjugated π-bond. For as long as those bonds are in the same plane, you can have a meaningful interaction between the π-orbitals.
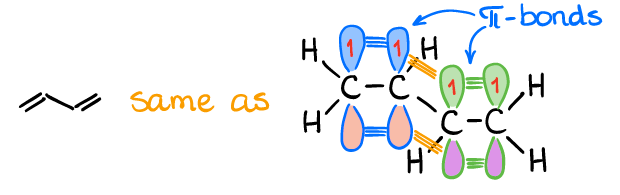
Using the LCAO principle that we talked about in the previous topic, we can construct 4 MO’s since there are 4 p-AO’s that are interacting with each other. For the simplicity sake, we always keep our MO’s represented as the initial p-orbitals. While we can draw the actual shapes for the MO’s that result from those interactions, those pictures will make understanding of the orbital interactions more complicated.
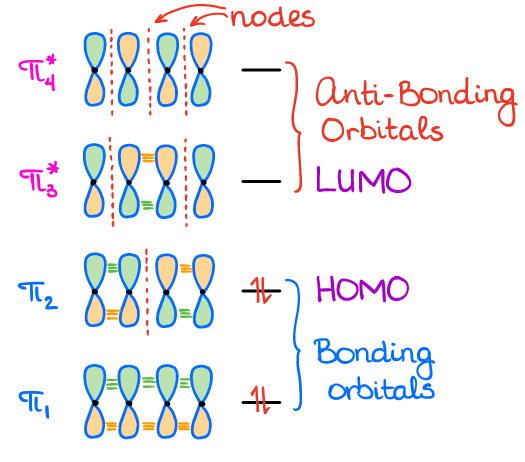
The lowest orbital in a conjugated system will always have all orbitals in the same phase. This orbital also has no nodes. Once we start going up in energy, we’ll start adding nodes which will cause the orbitals to change the phase. Notice, we always add nodes in a symmetrical fashion beginning at the center of the orbital.
Occasionally, drawing out the orbitals can be a bit tedious. We can use the shortcut by only showing the phase of one lobe of the orbital using the “+” or a “–“ signs.
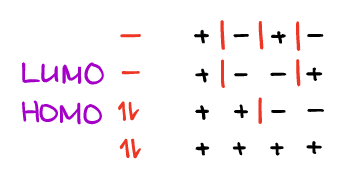
Before you use this shortcut, however, make sure that your professor is ok with that. While most professors will understand what you’re talking about here, if you use the shortcut, the teaching assistants who usually do the bulk part of grading may not realize that that’s what you’re doing and take point from you. I’ll be using the shortcut occasionally through this course though.
IMPORTANT: the orbital phases are not the charges. While we may use the “+” and the “-“ signs to identify them, they have nothing to do with the charge.
Molecular Orbitals in an Allylic System
Normally, when we deal with an allylic system, we’re going to have either a cation, anion, or a radical. Therefore, you’re going to have a different number of electrons in the system. Due to that, you’ll need to pay close attention to which orbital is HOMO and which one is LUMO.
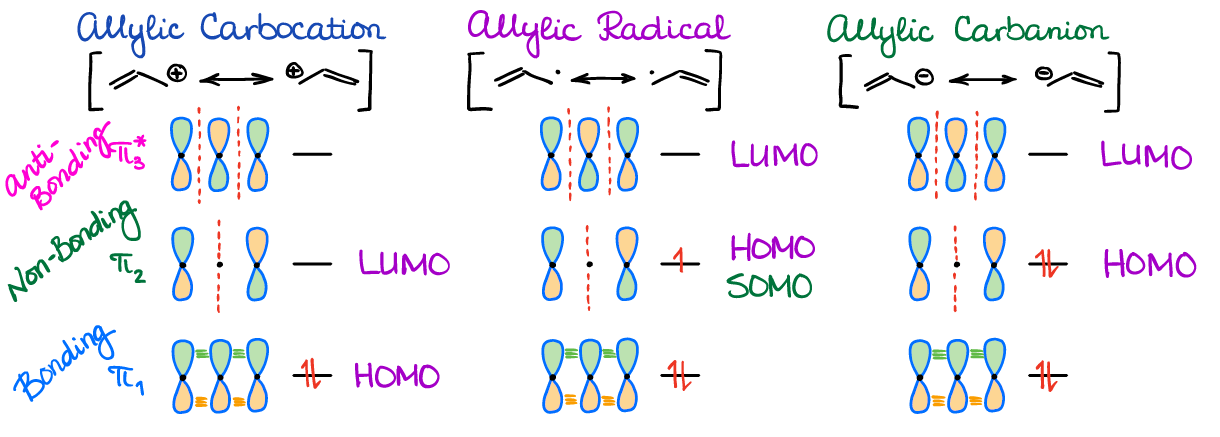
Notice how you have a non-bonding orbital here since the allylic system contains the odd number of atoms (3). There’s also a new abbreviation that I’m introducing here: SOMO. SOMO stands for Singly Occupied Molecular Orbital. SOMO is not a special orbital by any means. It’s just a fancy way of calling an orbital with an unpaired electron. SOMO also has no special properties or meaning for our purposes. However, some instructors like to emphasize it, so I thought I’d add it here too.
There are other types of allylic-like systems that you may see in your course. For as long as you have 3 atoms in a conjugated system supplying 3 p-orbitals, you’re always going to have the same orbital pictures as above. Can you come up with any other allylic-type systems?
Molecular Orbitals in 5- and 6-Atom Systems
The 5-atom systems are a bit exotic, although some instructors like to throw those on the exam or a homework. So, it’s a good idea to know how those look like.
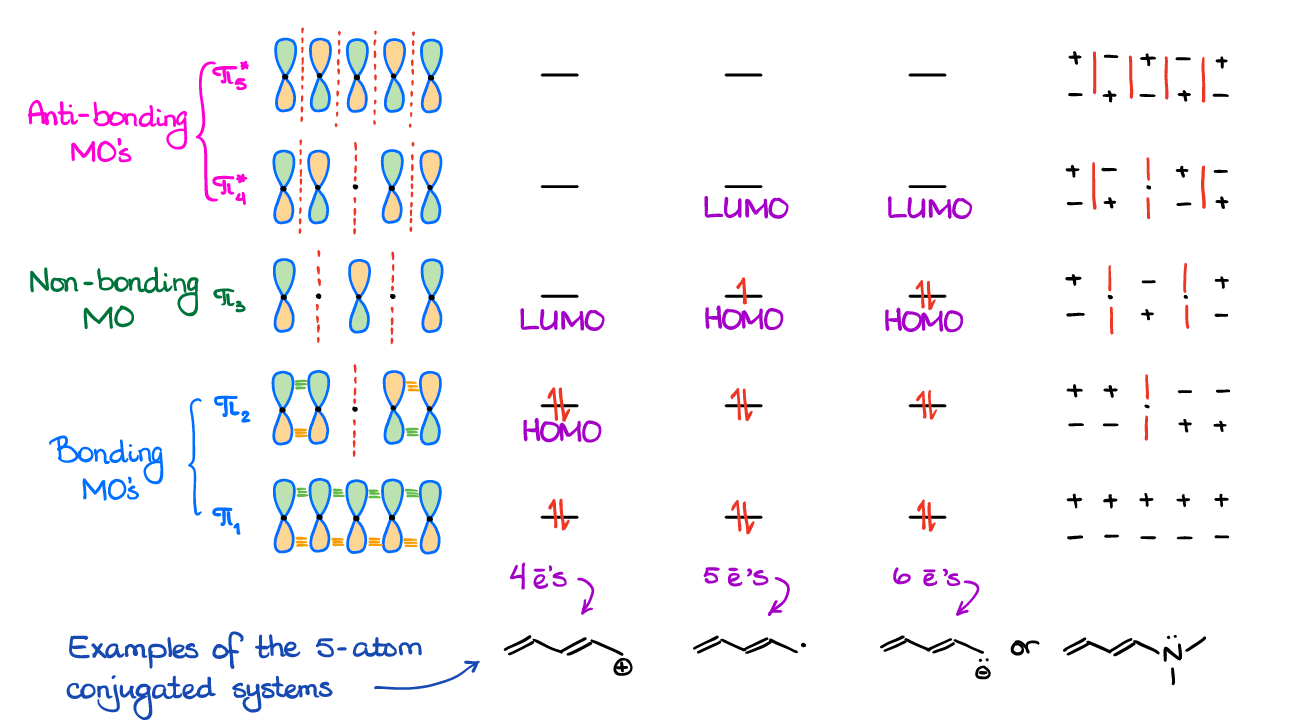
Like in the case with the allylic system, unless you have a heteroatom, you’re likely looking at an ionic species or a radical.
The 6-atom systems are, on the other hand, a very common “guest” on the test. You’ll also need to be able to use the MO’s of a 6-atom systems for some of the reactions of the conjugated systems.
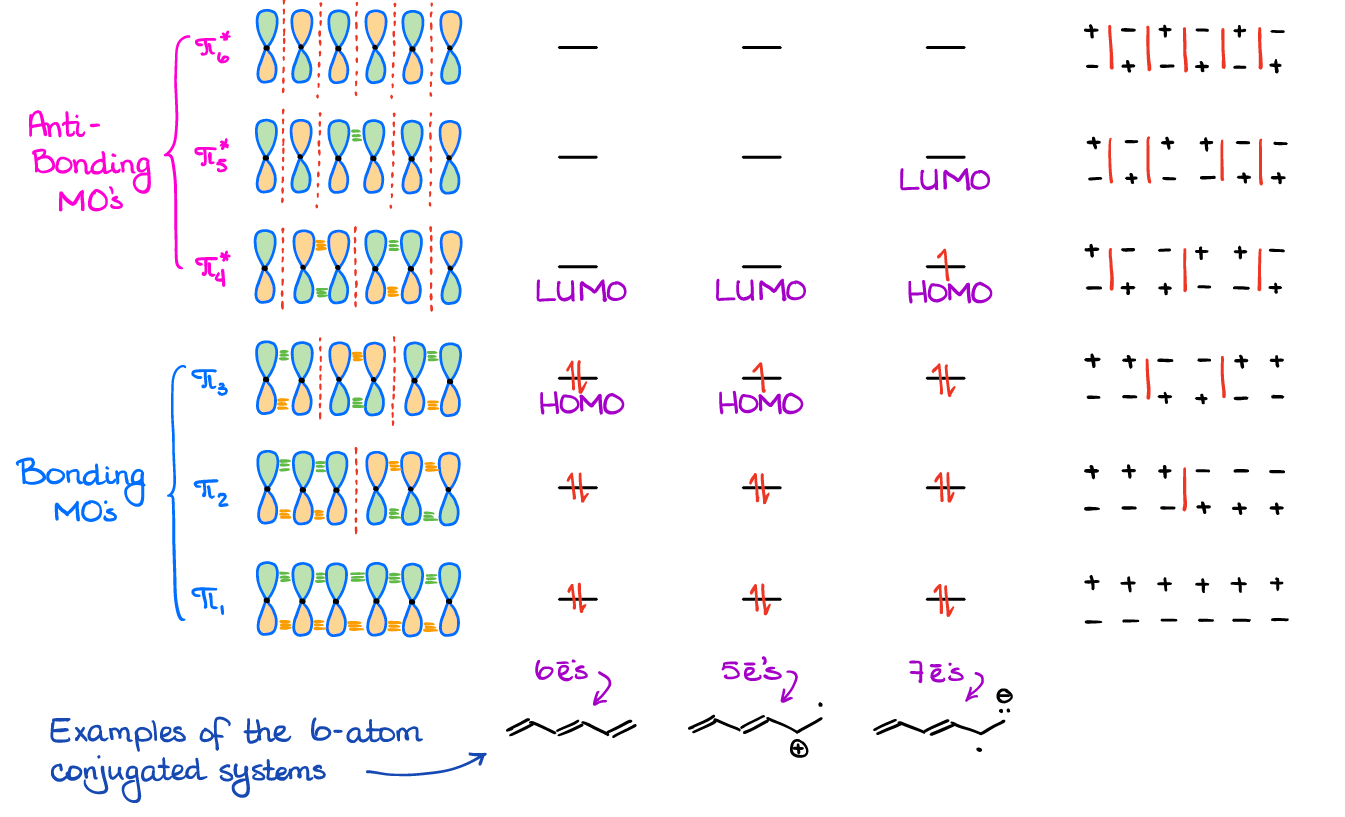
While the 6-atom system looks like a slightly more complicated case of the butadiene orbitals, I still urge you to practice drawing it a few times to make sure you can reproduce it from memory. Trust me, you’ll see it on the exam if your class covers any pericyclic reactions like Cope or Claisen rearrangement.