Conformational Analysis

In this tutorial, we will focus on the study of conformational analysis, which primarily involves Newman projections and chair conformations. Before you get to the nitty-gritty details of the conformational analysis, make sure you first review the tutorials on how to draw the Newman projections and chair conformations.

Conformations of Ethane

Ethane is one of the simplest hydrocarbons, yet it offers an intriguing look into the concept of molecular conformations. Let’s explore both its eclipsed and staggered conformations. We will also consider the energy differences between these conformations. Let’s get started.

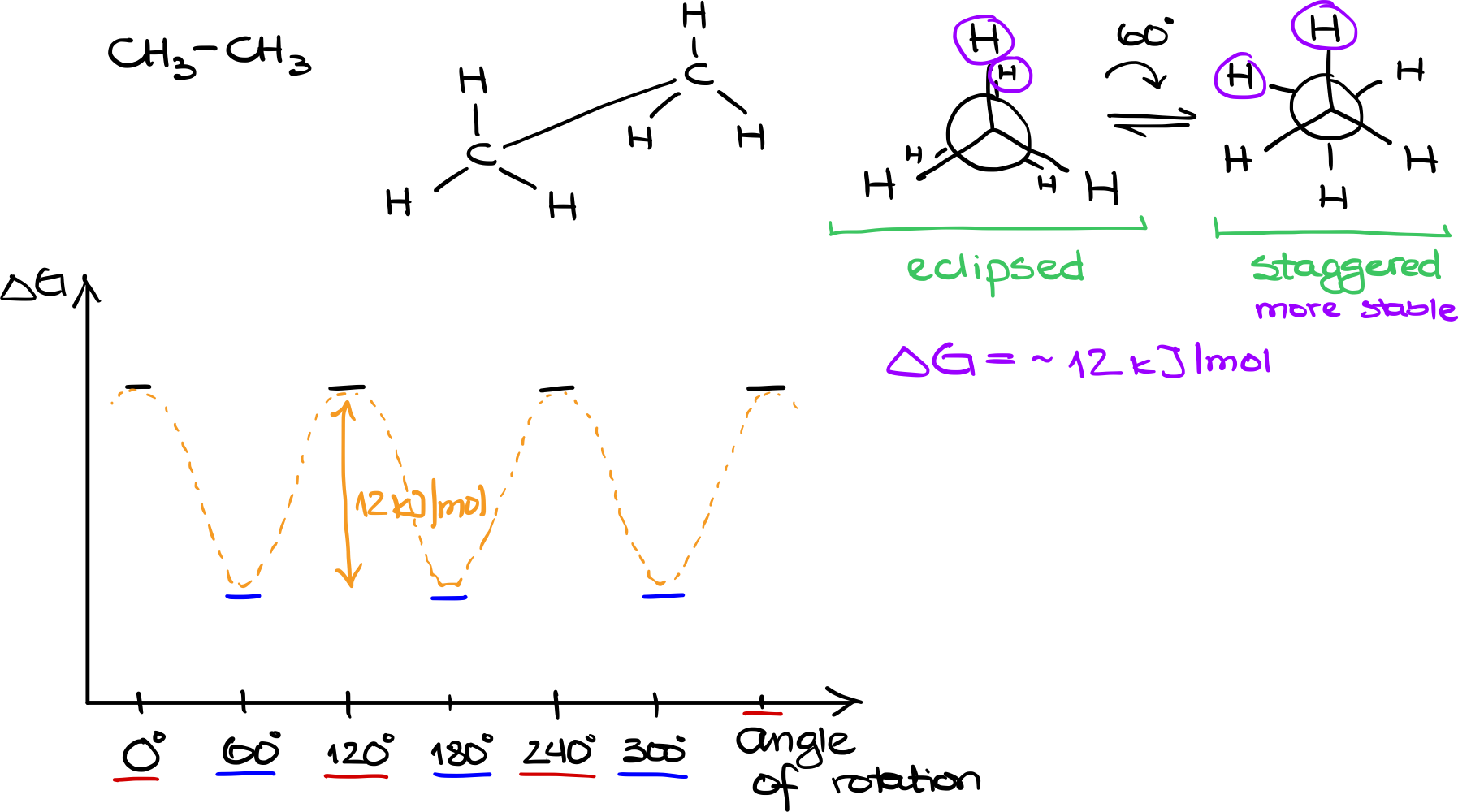
Molecular Structure of Ethane

Ethane has the molecular formula CH₃CH₃. Visualizing this molecule in 3D, each of the two carbon atoms is bonded to three hydrogens. If we were to draw a sawhorse projection, it would look like two tetrahedrons connected at their vertices.

Newman Projections of Ethane

For open-chain molecules like ethane, Newman projections serve as useful tools for visualizing conformations. In the case of ethane, the front carbon atom will have three hydrogens situated around it, and the back carbon atom will similarly be surrounded by three hydrogens. These hydrogens are staggered in a way that they ‘hide’ behind the hydrogens of the front carbon atom.

Types of Conformations

• Eclipsed Conformation

In the eclipsed conformation, the hydrogens on the front and back carbon atoms directly overlap each other. This results in a higher energy state due to increased electrostatic repulsion between the closely situated hydrogen atoms.

• Staggered Conformation

Alternatively, if we rotate the back carbon atom by 60°, the hydrogens from the back atom position themselves between the hydrogens of the front atom. This results in a staggered conformation, a lower energy state due to reduced electrostatic repulsion.

Energy Differences

When considering the stability of these conformations, it’s crucial to look at their energies. The eclipsed conformation is less stable because of the closer proximity of hydrogen atoms, leading to greater repulsion. On the other hand, the staggered conformation is more stable, with a difference in free energy (∆G) of approximately -12 kJ/mol.

Energy Diagram

If we plot these conformations on an energy diagram, with the vertical axis as the ∆G and the horizontal axis as the angle of rotation, we would see periodic peaks and valleys. Eclipsed conformations would be at 0°, 120°, 240°, and 360°, while staggered conformations would be at 60°, 180°, and 300°. Connecting these points, the curve smoothly oscillates, indicating the energy changes during rotation.

Conformations of Butane

While ethane’s conformational analysis is relatively straightforward, butane presents a bit more complexity. Let’s now analyze the butane’s conformations, depicted through Newman projections, and understand their energy differences.

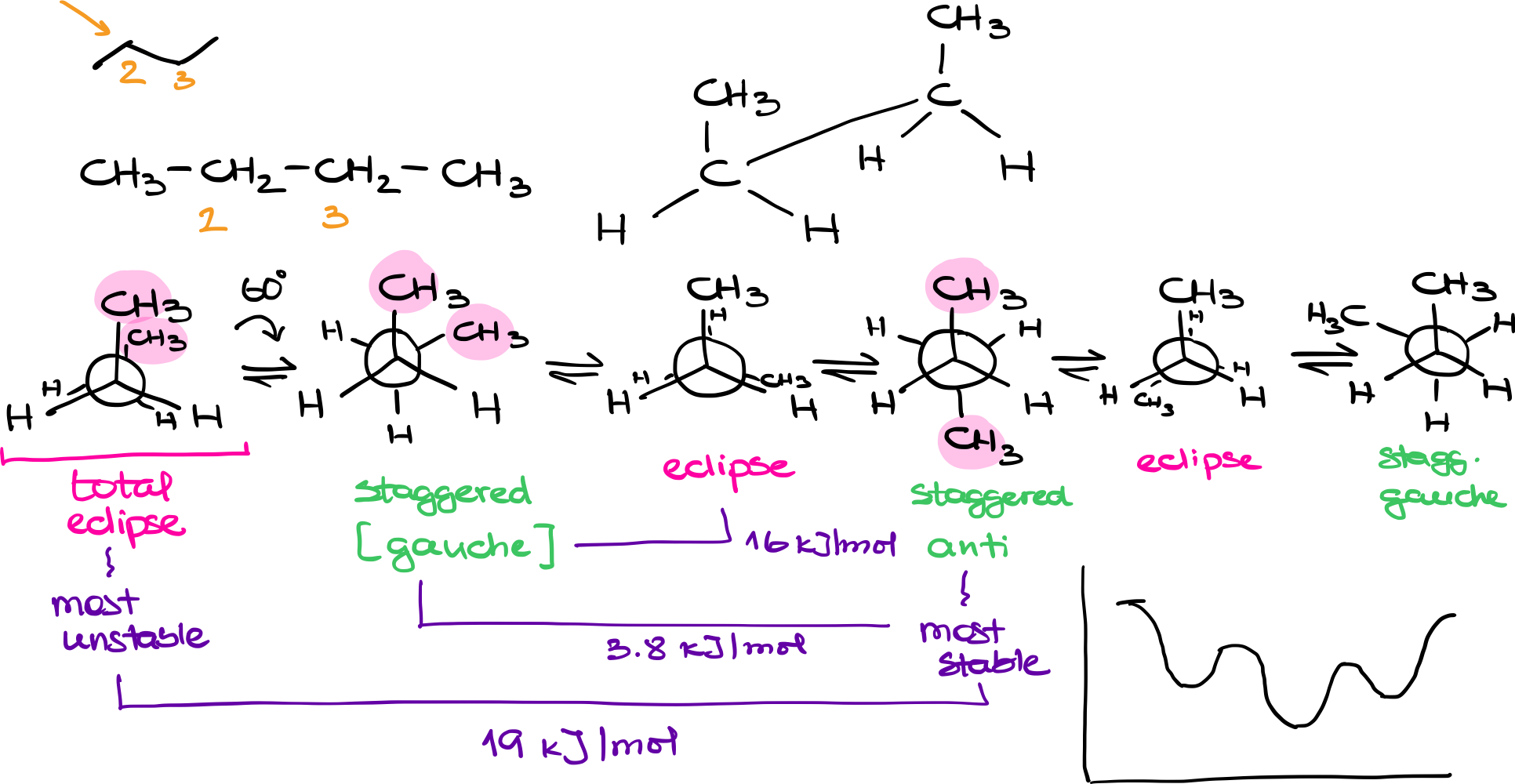
Molecular Structure of Butane

Butane consists of a linear carbon chain with the molecular formula CH₃CH₂CH₂CH₃. When analyzing its conformations, we often focus on the bond between the second and third carbons (C2 and C3), which have different substituents attached to them.

Newman Projections

In a Newman projection for butane, we look down the bond between C2 and C3. The front atom (C2) is attached to a -CH₃ group and two hydrogens. The back atom (C3) is also attached to a CH₃ group and two hydrogens. As we rotate the back atom while keeping the front atom fixed, we can visualize different conformations.

Key Conformations

• Total Eclipse: Both CH₃ groups are aligned directly behind each other. This is the most unstable conformation due to steric hindrance.
• Gauche: The CH₃ groups are at a 60-degree angle to each other. This is a staggered conformation that is lower in energy compared to any eclipse conformation but higher in energy compared to the anti-conformation.
• Regular Eclipse: One of the hydrogens on C2 aligns directly behind the CH₃ group on C3. This is an eclipsed conformation but not as unstable as the total eclipse.
• Anti: Both CH₃ groups are opposite each other. This staggered conformation is the most stable because it minimizes steric hindrance.

Energy Differences

Total Eclipse vs. Anti: ~19 kJ/mol

Anti vs. Gauche: ~3.8 kJ/mol

Gauche vs. Regular Eclipse: ~16 kJ/mol

These energy differences underline the importance of conformation in the stability of molecules. Staggered conformations are generally lower in energy than eclipsed conformations.

Energy Diagrams

When plotting the conformations on an energy diagram, you start with the highest energy level (total eclipse) and move through gauche, regular eclipse, and anti conformations, cycling back to the total eclipse. This gives a more nuanced picture of butane’s conformational landscape compared to simpler molecules like ethane.

More complicated example

To analyze the Newman conformations of a complex molecule like 2,4-dimethylpentane, we’ll follow a few steps methodically:

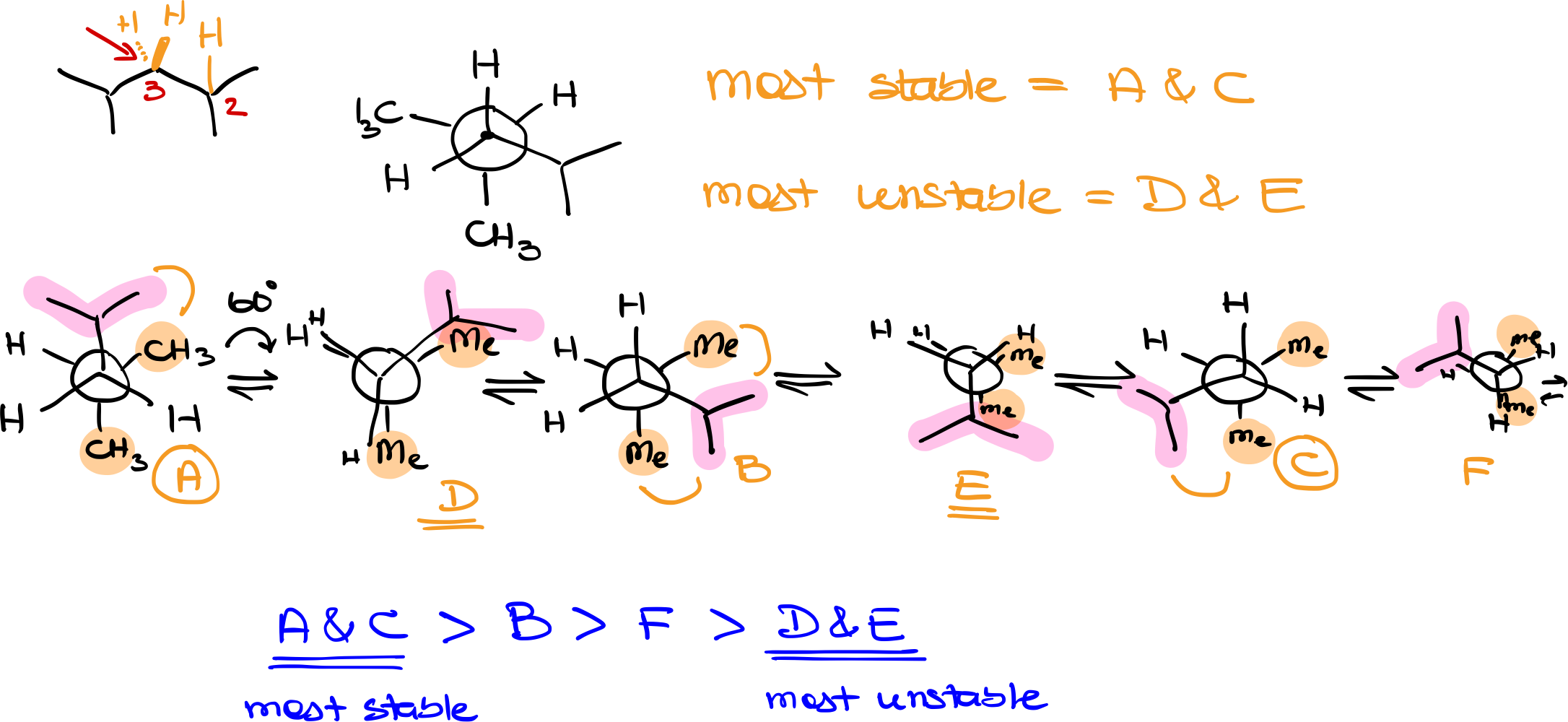
Step 1: Identification of Atoms and Bonds

First, identify the specific bond you’ll be examining. In 2,4-dimethylpentane, for example, you might look through the bond between carbons 2 and 3. Define one atom as the “front” and the other as the “back” for easier analysis.

Step 2: Identify Groups Around the Atoms

Next, determine the groups attached to the front and back atoms. In the front atom, we have an isopropyl group and two hydrogens. The back atom has two methyl groups and a hydrogen. These will be represented in the Newman projection.

Step 3: Initial Conformation

Choose an initial conformation to start with. For example, for this discussion, I’ll place the isopropyl group at the top and the methyl groups at random positions on the back atom. The hydrogen atoms will occupy the remaining spaces.

Step 4: Systematic Rotation

Begin rotating one of the atoms (either front or back) in 60-degree increments. This will help explore all possible conformations. You’ll end up with a series of staggered and eclipsed conformations. Label these conformations for easier reference (e.g., A, B, C, etc.).

Step 5: Analyzing Staggered Conformations

Staggered conformations are more stable than eclipsed ones. Look for the staggered conformation where the bulkiest groups are as far apart as possible. This will typically be the most stable conformation among the staggered set. Count the number of gauche interactions in each staggered conformation, as more gauche interactions generally indicate less stability.

Step 6: Analyzing Eclipsed Conformations

In the eclipsed conformations, identify where the bulkiest groups overlap, as these will be the least stable conformations. Label these for easier comparison (e.g., D, E, F, etc.).

Step 7: Ranking Stability

Once you have explored all possible conformations, rank them from most to least stable based on their spatial arrangement and the size of the groups. Generally, staggered conformations will be more stable than eclipsed ones, and among these, the one with the fewest gauche interactions will be the most stable.

Step 8: Review and Practice

Finally, remember to adhere to any specific instructions from your instructor or exam guidelines. Regular practice will solidify your understanding of this key concept in organic chemistry.

By adhering to this step-by-step process, you can systematically analyze and compare the Newman projections for complex molecules like 2,4-dimethylpentane, or even more complicated structures.

Chair Conformations

Understanding the conformations of cyclohexanes, particularly the chair conformations, is a critical aspect of organic chemistry. You’re going to see chair conformations quite often in your course and many instructors like to test the chairs on exams. Here, I’ll guide you through the process of determining which chair conformation is more stable.

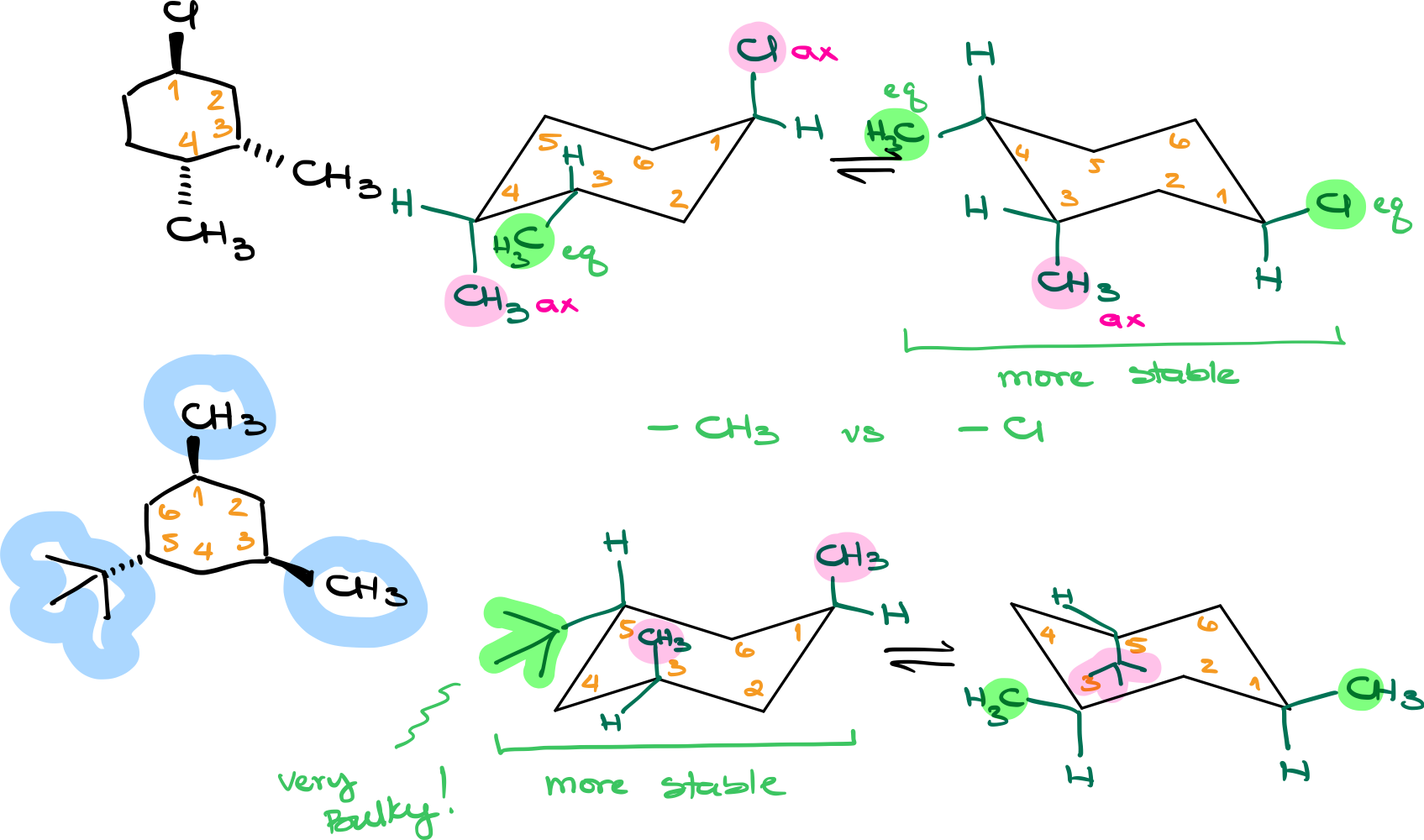
The Basics of Chair Conformations

Chair conformations are the most common spatial arrangements of cyclohexanes. They consist of alternating axial and equatorial positions for attached groups or substituents.

Step 1: Drawing Chair Conformations

• Start by drawing the skeletal structure of the chair conformation.
• Number the carbons consistently for easy identification.
• Add the substituent groups, indicating their positions as axial or equatorial.

Step 2: Finding the Most Stable Conformation

Look for the conformation where the bulkiest groups are equatorial. Generally speaking, you want to have as many bulky groups in the equatorial positions as possible. If all your groups are roughly the same in size, then look at the number of equatorial groups. If you have an extremely bulky group, such as a tert-butyl, phenyl, or isopropyl, prioritize this group in the equatorial position over the smaller groups.

Key Takeaway

When determining the stability of chair conformations:

• Always draw both chair conformations.
• Assign groups onto the corresponding positions in the chair and determine if they are axial or equatorial.
• Check the relative sizes of the groups. For significantly bulkier groups, prioritize their placement in the equatorial position for maximum stability.

By following these guidelines, you’ll be better equipped to tackle questions related to the stability of chair conformations in cyclohexanes.

To expand on the stability of different conformations and conformational analysis, we can also calculate the energy differences between the conformations. However, it’s a conversation for another day 😆

If you have any questions or feedback, please leave them in the comments below!